Practice with Similar Triangles
| Site: | Saylor Academy |
| Course: | GKT101: General Knowledge for Teachers – Math |
| Book: | Practice with Similar Triangles |
| Printed by: | Guest user |
| Date: | Tuesday, July 1, 2025, 9:45 AM |
Description
Complete these exercises and check your answers.
Review
1. Explain why all \(30-60-90\) triangles are similar.
2. The ratio between the sides of any \(30-60-90\) triangle is ________:________:________.
Find the missing sides of each triangle:
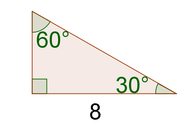
3.

[Figure 11]
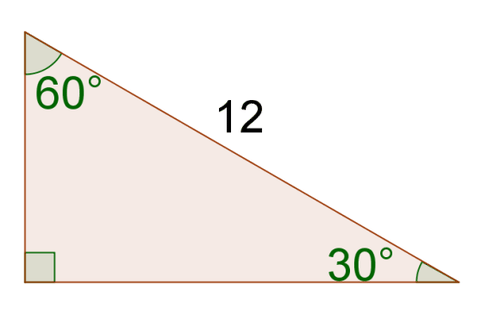
4.

[Figure 12]
5.

[Figure 13]
6. Explain why all \(45-45-90\) triangles are similar.
7. The ratio between the sides of any \(45-45-90\) triangle is ________:________:________.
Find the missing sides of each triangle:
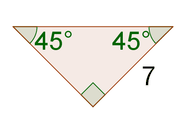
8.

[Figure 14]
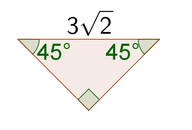
9.

[Figure 15]
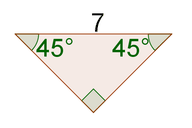
10.

[Figure 16]
Use the figure below for #11 and #12.

[Figure 17]
11. Prove that \(\begin{align*}\triangle ABC \sim \triangle EFD\end{align*}\).
12. Find the value of \(\begin{align*}x\end{align*}\).
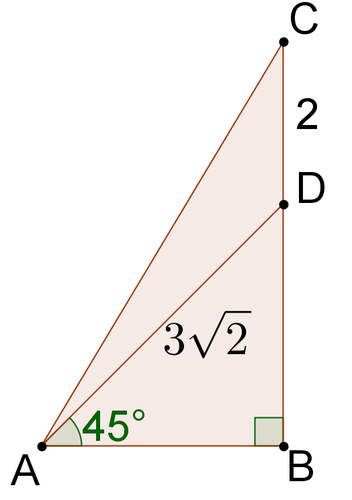
Use the figure below for #13-#15.

[Figure 18]
13. Find \(\begin{align*}m \angle ADB\end{align*}\). What type of triangle is \(\begin{align*}\triangle ADB\end{align*}\)?
14. Find \(\begin{align*}BD\end{align*}\) and \(\begin{align*}AB\end{align*}\).
15. Find \(\begin{align*}AC\end{align*}\).
16. A forest ranger sticks a walking stick that's 2 meters long vertically in the flat ground. The stick casts a shadow that's \(3\) meters long. She measures the shadow of a redwood tree nearby. It's \(20\) meters long. Create a diagram of the situation, showing the two right triangles which model the two objects and their shadows. Are these triangles similar? Why or why not? Are their sides proportional? If so, write and solve a proportion to find the height of the tree.
17. True or false: On a sunny day on flat ground, all vertical segments near me cast shadows that form right triangles. All these triangles are similar. As the sun rises or sets, the acute angles of these triangles change accordingly. Explain with a diagram.
 This work is licensed under CK-12 Curriculum Materials License.
This work is licensed under CK-12 Curriculum Materials License.Review - Answers
1. They have two pairs of congruent angles so they are similar by \(A A \sim\).
2. \(1: \sqrt{3}: 2\)
3. The missing sides are 6 and \(6 \sqrt{3}\).
4. The missing sides are \(8 \sqrt{3}\) and \(16\).
5. The missing sides are \(\frac{8}{\sqrt{3}}\) and \(\frac{16}{\sqrt{3}}\).
6. They have two pairs of congruent angles so they are similar by \(A A \sim\).
7. \(1: 1: \sqrt{2}\)
8. The missing sides are both length \(3\).
9. The missing sides are \(7\) and \(7 \sqrt{2}\).
10. The missing sides are both \(\frac{7}{\sqrt{2}}\).
11. Due to parallel lines, \(\angle C B A \cong \angle D F A\) and \(\angle C A B \cong \angle D E B\). The triangles are similar by \(A A \sim\).
12. The scale factor is 2. \(x=8\).
13. \(m \angle A D B=45^{\circ}\). \(\triangle A D B\) is an isosceles right triangle.
14. \(B D=A B=3\).
15. \(A C^{2}=3^{2}+5^{2} \cdot A C=\sqrt{34}\).